This post is the last in a series of four on boxplots and some of their extensions. Previous posts in this series have discussed basic boxplots, modified boxplots based on a robust asymmetry measure, and violin plots, an alternative that essentially combines boxplots with nonparametric density estimates. This post introduces beanplots, a boxplot extension similar to violin plots but with some added features. These plots are generated by the beanplot command in the R package of the same name and the purpose of this post is to introduce beanplots and briefly discuss their advantages and disadvantages relative to the basic boxplot and the other variants discussed in previous posts.
One of the examples discussed in Chapter 13 of Exploring Data is based on a dataset from the book Data by D.F. Andrews and A.M. Herzberg that summarizes the prevalence of bitter pit in 42 apple trees, including information on supplemental nitrogen treatments applied to the trees and further chemical composition data. Essentially, bitter pit is a cosmetic defect in apples that makes them unattractive to consumers, and the intent of the study that generated this dataset was to better understand how various factors influence the prevalence of bitter pit. Four supplemental nitrogen treatments are compared in this dataset, labeled A through D, including the control case of “no supplemental nitrogen treatment applied” (treatment A). To quantify the relationship between the prevalence of bitter pit and the other variables in the dataset, the discussion given in Exploring Data applies both classical analysis of variance (ANOVA) and logistic regression, but much can be seen by simply looking at a sufficiently informative representation of the data. The figure above shows four different visualizations of the percentage of apples with bitter pit observed in the apples harvested from each tree, broken down by the four treatments considered. The upper left plot gives side-by-side boxplot summaries of the bitter pit percentage for each tree, with one boxplot for each treatment. These summaries were generated by the boxplot command in base R with its default settings, and they suggest that the choice of treatment strongly influences the prevalence of bitter pit; indeed, they suggest that all of the “non-control” treatments considered here are harmful with respect to bitter pit, increasing its prevalence. (In fact, this is only part of the story here, since two of these treatments substantially increase the average apple weight, another important commercial consideration.) The upper right plot in the above figure was generated using the adjbox command in the robustbase package that I discussed in the second post in this series. In this modified display, the boxplots themselves are generally the same as in the standard representation (i.e., the heavy line still represents the median and the box in the center of the plot is still defined by the upper and lower quartiles), but outliers are flagged differently. As noted, this difference can lead to substantially different boxplots in cases where the data distribution is markedly asymmetric, but here, the adjbox plots shown in the upper right are identical to the standard boxplots shown in the upper left.
The lower left plot in the above figure was generated by the wvioplot command in the R package of the same name, using its default parameters. Arguably, this display is less informative than the boxplots shown above it, but – as discussed in conjunction with the Old Faithful geyser data in my last post and illustrated further in the next figure - the problem here is not an inherent limitation of the violin plot itself, but rather a mismatch between the default parameters for the wvioplot procedure and this particular dataset. Finally, the lower right plot shows the corresponding results obtained using the beanplot command from the beanplot package, again with the default parameters. Like the violin plot, the beanplot may be regarded as an enhanced boxplot where the box is replaced with a shape generated from a nonparametric density estimate, but there are some important differences, as these two plots demonstrate. First and foremost, the beanplot procedure permits the use of a variety of different kernel functions for density estimation, and it provides a variety of data-based bandwidth estimation procedures; in contrast, the wvioplot procedure uses a fixed kernel and a constant bandwidth parameter that may be specified by the user. Second, the beanplot procedure automatically includes a dashed horizontal line at the average overall response value for the dataset, along with heavy, solid horizontal lines at the average for each subset, and “beanlines” corresponding to the values of each individual observation within each “bean” of the beanplot. As the following examples illustrate, these beanlines can become an annoying distraction in large datasets, but they are easily excluded from the plot, as discussed below. Finally, another extremely useful feature of the beanplot procedure is that it has a built-in procedure to automatically determine whether a log transformation of the response axis is appropriate or not, although this option fails if the dataset contains more than 5000 observations, a point discussed further at the end of this post. For the bitter pit example, the beanplot in the lower right portion of the above figure gives the most detailed view of the dataset of any of the plots shown here, suggesting that the prevalence of bitter pit is very low for treatment A (i.e., the control case of no applied supplemental nitrogen treatment), as noted before, but also that many of the trees receiving treatment C exhibit very low levels of bitter pit as well, a conclusion that is not obvious from any of the other plots, but which is supported by a careful examination of the numbers in the dataset.
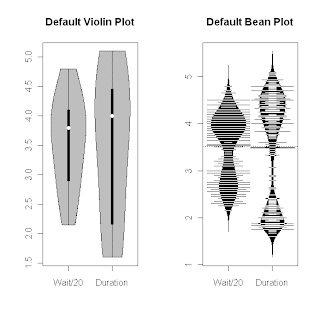
As I showed in my last post, the default parameter settings for the wvioplot procedure do not reveal the pronounced bimodal character of either the Old Faithful eruption durations or the waiting times between eruptions, although this can be seen clearly if the smoothing bandwidth parameter adjust is changed from its default value of 3 to something smaller (e.g., 1). The above figure shows the results obtained for these two data sequences – specifically, for the eruption durations and the waiting times between eruptions divided by 20 to make them numerically comparable with the duration values – using default parameter values for both the wvioplot procedure (left-hand plot) and the beanplot procedure (right-hand plot). As noted, the violin plot on the left gives no indication of these bimodal data distributions, while the beanplot on the right clearly shows the bimodal character of both data distributions. This difference reflects the advantages of the data-driven bandwidth selection feature incorporated into the beanplot package, although this feature can fail, a point discussed further at the end of this post. The above beanplots also demonstrate that the beanlines can become annoying in large datasets: in this case, the dataset contains 272 observations for each variable.
The above figure illustrates this difficulty even more clearly. The beanplot on the left shows the results obtained when the default beanplot procedure is applied to compare the four industrial pressure data sequences discussed in Chapter 1 of Exploring Data. In this example, each pressure dataset contains 1,024 observations, and the presence of this many beanlines in the left-hand beanplot results in a display that is ugly enough to be distracting. A much better view of the data is obtained by omitting the beanlines, easily done in the beanplot command by specifying the option what=c(1,1,1,0) – this retains the dashed line for the mean of all four pressure sequences (the first “1”), the beanplots themselves (the second “1”), and the heavy lines at the average for each bean (the third “1”), but it omits the individual beanlines (the final “0”). In particular, note that the bean averages are not even visible in the left-hand display, since they are completely obscured by the individual beanlines. Also, note that this example illustrates the automatic log scaling option mentioned above: here, the beanplot command generates a plot with logarithmic scaling of the pressure values automatically, without having to specify log = “y” as in the other displays considered here.
Finally, the plot above demonstrates the ability of the beanplot procedure to give insight into the dependence of a response variable on two different explanatory categories. This example is based on the mtcars dataset from the data collection included with the base R installation. This dataset characterizes 32 automobiles based on results presented in 1974 in Motor Trend magazine, and the beanplots shown here summarize the dependence of the horsepower of these automobiles on the number of cylinders in the engine (4, 6, or 8) and the type of transmission (“A” for automatic, or “M” for manual). Here, the dashed line corresponds to the average horsepower for all 32 cars, which is just under 150. Because this dataset is small (32 observations), the beanlines are quite informative in this case; for example, it is clear that all of the 4-cylinder engines and almost all of the 6-cylinder engines generate less than this average horsepower, while all of the 8-cylinder engines generate more than this average horsepower. These beanplots also show clearly that, while the mtcars collection includes few manual-transmission, 8-cylinder cars, these few exhibit the highest horsepower seen. The real point of this example is that, in favorable cases, beanplots can give us a great deal of insight into the underlying structure of a dataset. That said, it is also important to emphasize that beanplots can fail in ways that simpler data characterizations like boxplots can’t. As a specific example, a situation that arises commonly in practice – both for small datasets and for large ones – is that one of the subsets we want to characterize exhibits a single response value (this is obviously the case when the subset consists of a single observation, but larger data segments can also exhibit this behavior). Unfortunately, this situation causes a failure of the nonparametric density estimator on which the beanplot procedure is based; in contrast, boxplots remain well-defined, simply collapsing to a single line. Other potential difficulties with the beanplot package include the complication of too many beanlines in large datasets discussed above, and the fact that the automatic log scaling procedure fails for datasets with more than 5000 observations, but both of these difficulties are easily overcome by specifying the appropriate parameter options (to turn off automatic log scaling, specify log= “”).
Historically, boxplot summaries have been quite popular – and they remain so – largely because they represent a simple, universally applicable way of visualizing certain key features of how the distribution of a continuous-valued variable changes across groups defined by essentially any explanatory variable of interest. In its simplest form, this characterization is based on Tukey’s 5-number summary (i.e., the minimum, lower quartile, median, upper quartile, and maximum) and it remains well-defined for any continuous-valued variable. Like all simple, universally-applicable data characterizations, however, the boxplot cannot be complete and it can hide details that may be extremely important (e.g., bimodal distributions). For this reason, various extensions have been developed, aimed at conveying more details. Some of these extensions – like the variable-width boxplots discussed in the first post in this sequence – are also essentially always applicable, but others may not be appropriate for all datasets. In particular, strong distributional asymmetry may cause standard boxplot outlier detection rules – which treat upper and lower outliers equivalently – to perform poorly, and this has led to the development of extensions like the adjbox procedure in the robustbase package in R, discussed in the second post in this sequence. Although they are more complicated to compute, nonparametric density estimates can be much more informative than boxplots, and this has motivated the development of techniques like the violin plot discussed in my previous post and the beanplots discussed here, which both attempt to combine the simple interpretability of boxplots with the additional information available from nonparametric density estimates. Besides computational complexity issues, these more complicated visualization techniques can fail to yield any results at all, something that never happens with boxplots. For these reasons, I typically like to start with beanplot characterizations because, if beanplots can be constructed, they are potentially the most informative of the characterizations considered here. For large datasets, I try to remember to turn off the beanlines so I get informative beanplots and, if the dataset contains more than 5000 observations, to specify log = “” ( or log = “y” if I want a log-transformed display) so that I get any beanplots at all. In cases where the beanplot procedure fails, I go back to either a standard or adjusted boxplot, or else I construct both and compare them to see whether they are suggesting different sets of points as outliers. In any case, I typically use the variable width option in generating boxplots to see how well balanced the data subsets are that I am comparing. Generally, I find that by constructing a few plots I can get a useful idea of how a continuous-valued response variable behaves with respect to a variety of potential explanatory variables.



Thanks for this. It is always interesting to find another way of presenting the information.
ReplyDeleteThis post was not as clear as the other three for me. But, informative nevertheless. Thanks.
ReplyDeleteVery clear, thanks!
ReplyDelete
ReplyDeleteWe really love such writtings as they are a great motivation to us thanks alot
comprar percocet linea
BUY Greenstone Xanax ONLINE
BUY Greenstone Xanax ONLINE
Buy Sodium Cyanide Online
ReplyDeleteWe really love such writtings as they are a great motivation to us thanks alot
comprar percocet linea
buy ADDERALL AUSTRALIA
buy RITALIN CHINA
buy vyvanse online
BUY Greenstone Xanax ONLINE
buy vyvanse online
Buy Actavis Cough Syrup
ReplyDeleteWe really love such writtings as they are a great motivation to us thanks alot
comprar percocet linea
buy ADDERALL AUSTRALIA
buy RITALIN CHINA
buy vyvanse online
BUY Greenstone Xanax ONLINE
buy vyvanse online
Buy Actavis Cough Syrup
BUY Greenstone Xanax ONLINE
BUY Greenstone Xanax ONLINE
https://sites.google.com/view/sbobetonline365/bola88
ReplyDeleteJudi Bola Online sbobet
https://educatorpages.com/site/judibola88/pages/situs-judi-online
ReplyDeleteSitus Judi Online sbobet 2021
https://judibola88.educatorpages.com
ReplyDeleteSitus Judi Online deposit pulsa
https://mainjudionline.mystrikingly.com
ReplyDeleteSitus Judi Online 2021 paling hoki
https://mainjudionline.company.site
ReplyDeleteSitus Judi Online gampang menang
https://sites.google.com/view/ayomain/judionline
ReplyDeleteSitus Judi Online terbaik 2021 di Indonesia dengan permainan terlengkap
https://manilabet365.weebly.com
ReplyDeletesitus Judi Online terpercaya 2021
buy-seconal-sodium
ReplyDeletebuy-sodium-cyanide
acheter percocet
acheter de loxycodone
morphine
acheter du suboxone
acheter du fentanyl
buy-seconal-sodium
ReplyDeletebuy-sodium-cyanide
acheter percocet
acheter de loxycodone
morphine
acheter du suboxone
acheter du fentanyl
buy-seconal-sodium
ReplyDeletebuy-sodium-cyanide
acheter percocet
acheter de loxycodone
morphine
acheter du suboxone
acheter du fentanyl
ReplyDeleteI love the way you write and share your niche! Very interesting and different! Keep it coming!buy vyvanse online
Awesome! Its really amazing post, I have got much clear idea on the topic from this post. 중국야동넷
ReplyDeletePlease visit once. I leave my blog address below
야설
중국야동넷
I really enjoy your web’s topic. Very creative and friendly for users. Definitely bookmark this and follow it everyday.
ReplyDelete바카라사이트
บริการเกมสล็อตออนไลน์ปี 2022 เกมให้เลือกเล่นมากกว่า 1,000 เกม 1รับ20 เมก้า เล่นได้จริง แจกจริง สมัครเลยตอนนี้*********
ReplyDeleteWhether I'm looking for tips, advice, or inspiration, I always find what I need here. Oke4d
ReplyDeleteI appreciate the positivity and encouragement you bring to your blog. Keep up the great work! Markastoto
ReplyDelete